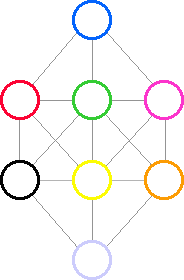
I first came across this clever puzzle in Martin Gardner's excellent book "Further Mathematical Diversions". It had been used to illustrate the fact that by using a logical approach it is possible to quickly derive a solution to a problem that would be difficult to solve by a brute force method - such as that which might be tried using a computer - of trying every one of the 40,320 possible arrangements until the unique solution (apart from upside down and mirror image forms) was found.

The digits from 1 to 8 are to be placed in the eight circles shown in the figure above. There is one condition that must be kept and that is that no two digits that are next to each other in serial order may go in circles that are directly connected by a line. So if 5 were placed in the top circle then neither 4 nor 6 may be placed in any of the three circles that form the horizontal row beneath it.
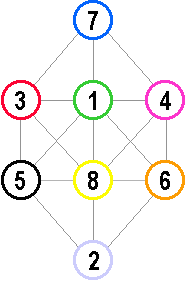
In the series 1 to 8 each digit has two neighbours except 1 and 8. In the diagram the green circle is connected to every other circle except the purple one at the bottom. So if the green circle were to contain any of the numbers 2, 3, 4, 5, 6, 7 then the purple circle would have to accomodate both the adjacent numbers. This is impossible so the green circle must contain either 1 or 8, and by a similar argument the yellow circle must contain the other one. So let's put 1 in the green circle and 8 in the yellow circle. The purple circle at the bottom must now contain 2 and the blue circle at the top must contain 7. The remaining four numbers are now easily placed.
| Back to the Mindbenders |