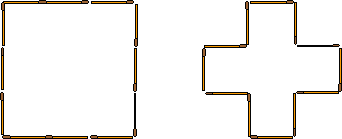
Back in the days when smoking was popular it was common to find puzzles that involved rearranging matches to form different shapes. Here is a tricky one that Pythagoras would probably have been proud of. I first came across this puzzle in Martin Gardner's superb book "Mathematical Puzzles and Diversions".
There are actually hundreds of different solutions to this problem! Here are some of the most elegant.
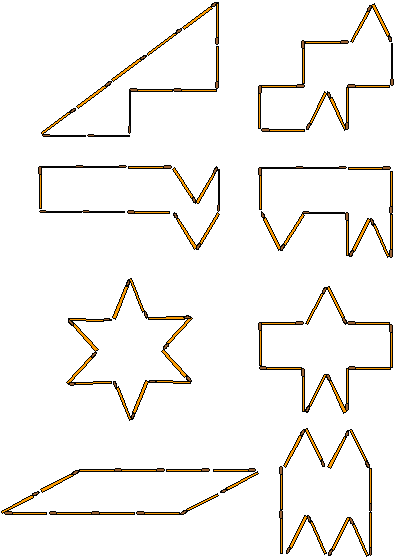
The shape in the top left is produced by first creating a pythagorean right angled triangle with sides 3, 4 and 5 - this has an area of 6 square units. Then rearrange three of matches to reduce the area by 2 square units.
Many of the other polygons are based on tetrominoes. These are the shapes you can make by placing four squares next to each other. A tetromino will therefore have an area of four square units. If you use the matches to produce the outline of a tetromino you will have some matches left over. So to use up all the 12 you just add and subract similar triangle shapes. The polygon on the left in the second row has been created this way from a tetromino of four squares in a straight line.
A regular six-pointed star shape will have an area between 0 and 11.196 square units (the area of a regular dodecagon) depending on how far apart the points that make up the base of each of its six constituent triangles are. If you set this at 0.821 units the star will have an area of 4 square units.
 Back to Boston United Home Page. |
Back to the Mindbenders |